Introduction to Symbolic Logic

⊕ PHI 333: Introduction to Symbolic Logic
Required for the Philosophy Major
Satisfies an Area I requirement for the Symbolic, Cognitive and Linguistic Systems Certificate


This course is an introduction to symbolic logic. It is designed to provide an understanding of symbolic techniques for representing and evaluating sentences, arguments, and theories.

Sentences, arguments, and theories are objects you take into your mind throughout your life. Some are good for you. Some are not. Symbolic logic can help you know the difference.

Assignments and Grades

The grade for the course is a function of six homework assignments (68 points), a midterm examination (10 points), a final examination (10 points), and six debriefing sessions (12 points).

Grades for the assignments sum to the grade for the course: A+ (100-97), A (96-94), A- (93-90), B+ (89-87), B (86-84), B- (83-80), C+ (79-77), C (76-70), D (69-60), E (59-0).

Unit 1. Atomic Sentences
• Homework 10 points, Debriefing 2 points

Unit 2. Boolean Connectives
• Homework 10 points, Debriefing 2 points

Unit 3. Formal Proofs involving Boolean Connectives
• Homework 15 points, Midterm examination 10 points, Debriefing 2 points

Unit 4. Quantifiers
• Homework 10 points, Debriefing 2 points

Unit 5. Methods of Proof for Quantifiers
• Homework 8 points, Debriefing 2 points

Unit 6. Formal Proofs involving Quantifiers
• Homework 15 points, Final examination 10 points, Debriefing 2 points

⊕ Natural deduction proofs are a large part of what students learn in introductions to symbolic logic. There are different ways to present these proofs. The Fitch style is a modern version of the presentation Stanislaw Jaśkowski introduced in 1934. The Gentzen style is the main alternative. It is the presentation Gerhard Gentzen introduced in the same year.

Language, Proof and Logic uses the Fitch style. This is the style of natural deduction most introductory courses use.

Here is a proof of ¬P∨¬Q ⊢ ¬(P∧Q) in the Fitch style written in the software in the LPL Course Package:




Here is a corresponding proof in the Gentzen style:




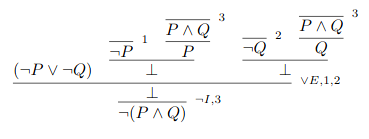
For discussion of the two styles, see Natural Deduction Systems in Logic (The Stanford Encyclopedia of Philosophy). There is no possibility for extra credit.
Late work will not be accepted without good reason. (If you are going to submit work late, I accept more reasons as good reasons if you contact me before the due date.)
I give incompletes only to accommodate serious illnesses and family emergencies.
I enjoy working with Barrett students on Honors Enrichment Contracts.

The LPL Course Package

The LPL Course Package is required for the course.
For learning logic, there is no better combination of written explanation, software, and videos.

The package is titled "Language, Proof and Logic (LPL)."
The paperless package works in your browser. The physical package includes a textbook.
You should buy the paperless package from the online store. The textbook is out of date.

The LPL Paperless Package includes the online grading service, Grade Grinder.
This service is required for the course You cannot get credit for the homework without it.

If you have questions about any of this, email me.

How to Do Well in This Course

The homework and the debriefing sessions are 80% of the final grade.

The debriefing sessions require only that you write something coherent about your experience.

The homework is harder, but Grade Grinder is your friend.
As part of their explanation of how to use this service, the authors offer the following advice:

"[Y]ou can always do a trial submission to see if you got the answers right,
asking that the results be sent just to you. When you are satisfied with your solutions,
submit the files again, asking that the results be sent to the instructor too" (9).

If you want a high grade in this course, take this advice.
Start early on the homework. Leaving it till the last minute is almost never the right choice.
Before the due date, use Grade Grinder to make sure your answers are correct.
If you are having trouble, post a question.

The homework takes time to understand and complete.
Learning logic is mastering a skill. No one is born with this skill. Everyone has to practice to acquire it.
The book contains more exercises than those assigned for homework.
The more you do, the more you master the skill.

To complete the homework assignments, you must use the software in the LPL Course Package: Boole, Fitch, Tarski's World, and Submit (the service that submits your work to Grade Grinder.) To learn how to use this software, I recommend that you read the documentation and watch the tutorial videos on the support page. You should also read the description of timestamps for file creation Grade Grinder uses a plagiarism detection mechanism.

The midterm and final examinations are multiple choice questions about concepts. I will tell you the concepts on which you will be tested. You have unlimited attempts for each exam until the due date.

If you post a question, the more detail you can provide the better.
You should include a screen shot if the question involves the course software.
Post again if you don't understand my answer or think I have not answered the question you posted.

I host periodic zoom sessions and am happy to meet individually by zoom. Email me.

Common Student Experiences

Students tend to have one of two experiences in this class.

Students who get an early start on the homework, and have the time to devote to the class, tend to do well.

Students who do not get an early start on the homework, and do not have much time to devote to this class, tend to do poorly. I have seen few if any exceptions to this rule. Logic takes time to learn.

It is not about intelligence.

Everyone at ASU is more than smart enough to learn logic at this level. It is about time to learn the skill. Learning logic is like learning to play a sport or a musical instrument. It takes practice, and practice takes time.

Contact Information:

Thomas A. Blackson, Philosophy Faculty
School of Historical, Philosophical, and Religious Studies
Lattie F. Coor Hall, room 3356
PO Box 874302
Arizona State University
Tempe, AZ. 85287-4302
Email: blackson@asu.edu
Academic Webpage: tomblackson.com